A new technique for the simulation of electronic systems at finite temperature by means of noisy QMC forces

The most common application of computer simulations is to predict the properties of materials. Since the first works, by Metropolis et al. and Fermi et al. (27,84), Molecular Dynamic (MD) techniques turned out to be a powerful tool to reproduce the properties of materials in different conditions and also to predict them.
The combination of these techniques with the density functional theory (DFT) has become a widely accepted and powerful ab-initio method: the Car-Parrinello Molecular Dynamics (CPMD) (54) that has allowed to study a broad range of chemical, physical and biological systems. The CPMD approach offers a balance of accuracy and computational efficiency that is well suited for both static and dynamic calculations of numerous properties of systems with hundreds and even thousands of atoms. Although in principle DFT is an exact theory for the electron correlation, it relies on an unknown exchange and correlation functional that must be approximated. The widely used Local Density Approximation (LDA) is difficult to improve systematically. Therefore, in some cases (see for instance Ref. (85)), one requires a more accurate computational approach, such as the quantum Monte Carlo (QMC) approach to solve the Schrödinger equation very accurately.
In this thesis, we present a new method that treats the electrons within the many-body QMC and perform Molecular Dynamic ''on the fly'' on the ions. This method provides improved dynamical trajectories and significantly more accurate total energies.
In the past two different approaches were proposed to couple Quantum Monte Carlo with ionic Molecular Dynamic. The first, called Coupled Electronic-Ionic Monte Carlo (CEIMC) (8), is based on a generalized Metropolis algorithm that takes into account the statistical noise present in the QMC evaluation of the Bohr-Oppenheimer surface energy. In the second approach, called Continuous Diffusion Monte Carlo (CDMC) (64), the Molecular Dynamics trajectories are generated with some empirical models or by CPMD-DFT, and then the CDMC technique is used to efficiently evaluate energy along the trajectories. Both methods present some drawbacks. In the second method even if all the properties are evaluated using the Diffusion Monte Carlo, the trajectories are generated using empirical models without the accuracy given by the QMC for the structural properties, as radial distribution, bonding lengths and so on. Instead, in the first one the QMC energies are used to perform the Monte Carlo sampling leading to accurate static properties. In order to have a reasonable acceptance rate within this scheme simulations have to be carryed out with a statistical error on the energy of the order of 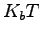$K_b T$ Furthermore, in order to have a fixed acceptance rate the amplitude of the ionic move has to be decreased with the size of the system.
The method we present here, allows to solve two major drawbacks of the previous two techniques. Following the idea of Car and Parrinello (54) we will show that it is possible to perform a feasible ab-initio Molecular Dynamics and structural optimization in the framework of the Quantum Monte Carlo by using noisy ionic forces, and with a method that do not contain any rejection scheme, at the expense of a time discretization error, that is present in any type of MD scheme.