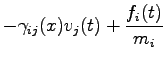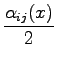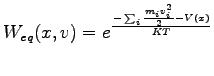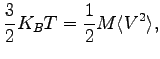Next: Numerical integration of the
Up: A new technique for
Previous: Dealing with Quantum Monte
Contents
In order to simulate the canonical ensemble we use a Langevin dynamics and we assume that our system is coupled with a thermal bath due to Quantum Monte Carlo statistical noise plus an additional friction term:
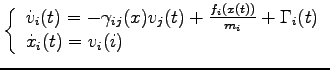 |
(5.4) |
with
where 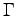 is a generic Gaussian noise that implicitly contains the one associated to the statistical evaluation of the forces by QMC. Notice that in this case an explicit dependence on
is a generic Gaussian noise that implicitly contains the one associated to the statistical evaluation of the forces by QMC. Notice that in this case an explicit dependence on 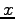 of the noise has been taken in account. This is a realistic case that has not been considered so far not even in (89). In the following we determinate a form for the friction matrix
of the noise has been taken in account. This is a realistic case that has not been considered so far not even in (89). In the following we determinate a form for the friction matrix
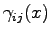 that allows to converge the usual Boltzmann distribution at a given temperature.
that allows to converge the usual Boltzmann distribution at a given temperature.
To this purpose we write down the corresponding Fokker-Planck equation. Following (90) we have to evaluate the drift and the diffusion coefficient:
A straightforward calculation shows that:
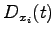 |
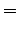 |
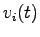 |
(5.9) |
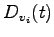 |
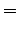 |
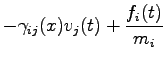 |
(5.10) |
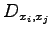 |
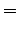 |
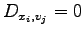 |
(5.11) |
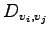 |
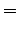 |
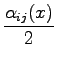 |
(5.12) |
And so the corresponding Fokker-Plank equation will be:
![$\displaystyle \frac{\partial W(x,v,t)}{\partial t} = \sum_i \left \{ \frac{\par...
...rac{\alpha_{ij}(x)}{2} \frac{\partial}{\partial v_j} \right ]\right \} W(x,v,t)$](img535.png) |
(5.13) |
Then the friction matrix
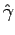 is chosen in a way that the stationary solution of the Fokker-Planck equation is the canonical distribution:
is chosen in a way that the stationary solution of the Fokker-Planck equation is the canonical distribution:
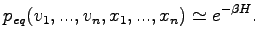 |
(5.14) |
More precisely by substituting the Boltzmann distribution
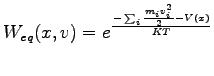 |
(5.15) |
in the equation 5.13 we obtain:
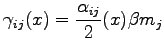 |
(5.16) |
So for a given noise on the forces
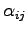 and the desired temperature we can set the friction tensor using eq. 5.16 in order to obtain the Boltzmann distribution.
and the desired temperature we can set the friction tensor using eq. 5.16 in order to obtain the Boltzmann distribution.
Notice that the external random noise scale as
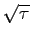 (see also Ref. (90)) whereas the QMC noise scales as
(see also Ref. (90)) whereas the QMC noise scales as 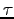 . Therefore in the limit
. Therefore in the limit
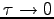 if we do not add any external noise and we set
if we do not add any external noise and we set
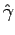 according to eq. 5.16, the system will converge to the Newton dynamics at zero temperature. Nevertheless adding an appropriate external noise it is possible equilibrate the system to the canonical ensemble at the desired temperature.
according to eq. 5.16, the system will converge to the Newton dynamics at zero temperature. Nevertheless adding an appropriate external noise it is possible equilibrate the system to the canonical ensemble at the desired temperature.
A peculiar feature of this approach is that in the limit of small 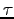 the statistical error on the forces becomes irrelevant because
the statistical error on the forces becomes irrelevant because
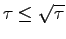 .
.
The stability of this approach compared with the first order Langevin Dynamic is now evident, in fact there is no need to calculate the inverse of the covariance matrix. Moreover in the second order Langevin Dynamics the temperature can be estimated at posteriori by equality:
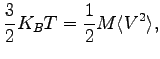 |
(5.17) |
compensating the error in the integration of the GLE.
Subsections




Next: Numerical integration of the
Up: A new technique for
Previous: Dealing with Quantum Monte
Contents
Claudio Attaccalite
2005-11-07
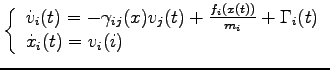
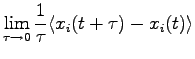
![$\displaystyle \frac{1}{2}\lim_{\tau \to 0} \frac{1}{\tau} \langle [x_i(t+\tau) -x_i(t)][x_j(t+\tau) -x_j(t)] \rangle$](img526.png)