Following the ionic dynamics

A reasonable approximation for the physical forces acting on the ions are the ones calculated when the electronic system is at the energy minimum with the chosen variational ansatz. Therefore in order to generate the correct dynamical trajectories for the ions it is extremely important to relax the trial function to the minimum energy at each ionic time step. As shown by different authors first-order optimization methods, as stochastic gradient or stochastic reconfiguration, defined by:

$$\dot{\psi} = S^{-1} \vec f,$$ (5.28)

where 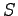$S$ is a positive definite matrix, and 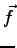$\vec f$ is the vector of the generalized forces eq. 2.11 fails to follow a second order dynamics (97). This causes a systematic error in the ionic forces, because the wave-function is not at the energy minimum.

To overcome this problem many techniques were used, such as Car-Parrinello dynamics ((54)), or conjugate gradients ((97)). In our work we used a new technique that is suited very much for energy optimization by means of Quantum Monte Carlo, the SRH method. The major advantage of this method is that it uses the information coming from the Hessian. Thanks to the Hessian matrix this method is able not only to follow the direction of the minimum but also to estimate the distance from the minimum for each parameter in such a way to converge in few steps. Moreover, if we start from an optimized trial function and we move the ions not too fast, we can maintain the system in a regime in which the quadratic approximation is always valid so that in principle the Hessian optimization converges always in one step.