Setting the parameters in the Langevin dynamics

Parameters of the Eq. 5.22 can be tuned in different ways according to what we want to simulate. As shown by Ref (88,87) the Generalized Langevin Dynamic allows to study dynamical properties with the condition that the friction term 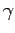$\gamma$ is small compared to the typical frequencies of the system, in fact too large 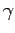$\gamma$ over-damps the low-frequency vibrational modes (see Ref. (95)). Therefore in order to have the desired small 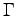$\Gamma$ the only possible solution is to increase the VMC bin length in such a way that the VMC noise decrease to the desired value.
On the other hand if only static properties are required it is possible to tune GLE parameters in a more efficient way. In fact, although by our method it is possible to work only with QMC noise, it can be convenient sometimes to add external noise to the forces for different reasons.
Let us imagine to simulate a system at high temperature. In that case there are two possibilities: either the bin length used to evaluate the forces has to be decreased in order to increase the QMC noise, or the friction has to be rescaled according to Eq. 5.16 that implies a corresponding reduction of the dissipation in the system. But both these solutions present some problems. In the first case one cannot decrease the bin length below a certain threshold otherwise the hypothesis of Gaussian noise is no longer fulfilled and the optimization algorithm becomes unstable; in the second case the use of a very small friction matrix leads to a long convergence time that is related to the smallest eigenvalues of the 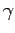$\gamma$ matrix $\tau \simeq \frac{1}{\gamma_{min}}$ .
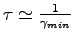For these reasons we found that is more convenient to add external noise to the system, in such a way to produce the desired temperature with a given bin length and to maintain the friction matrix not too small. To this purpose we have added a Gaussian noise with diagonal correlation matrix:

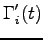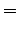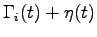$$\Gamma'_i(t) = \Gamma_i(t)+\eta(t)$$ (5.24)

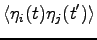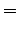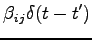$$\langle \eta_i(t) \eta_j(t') \rangle = \beta_{ij} \delta(t-t')$$ (5.25)

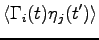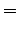$$\langle \Gamma_i(t) \eta_j(t') \rangle =$$ 0 (5.26)

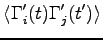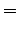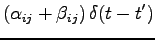$$\langle \Gamma'_i(t) \Gamma'_j(t') \rangle = \left ( \alpha_{ij} + \beta_{ij} \right ) \delta(t-t')$$ (5.27)

This procedure allows us to achieve the maximum efficiency when it is possible to set the 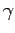$\gamma$ as close as possible to the critical dumping of the system (see Tassone, Car and Mauri Ref. (96)).