The Born-Oppenheimer approximation

The idea of treating ionic dynamics classically, while electrons are in the ground-state of the Hamiltonian 4.1, is based on two very reasonable approximations: the Born-Oppenheimer Approximation(BO) and the Adiabatic one.
In a system of interacting electrons and nuclei there will be usually small momentum transfer between the two types of particles due to their very different masses.

On the time-scale of nuclear motion, one can therefore consider the electrons to relax in the ground-state given by the Hamiltonian with the nuclei at fixed locations. This separation of the electronic and nuclear degrees of freedom is known as the Born-Oppenheimer approximation. Moreover since the energy scale associated with the electronic excitations is usually much larger than to the one related to the ionic motion, one can safely consider the electron in their own ground-state. Although this approximation is not always fulfillid even in the worst case, for the simulation of the lightest atom, hydrogen, Galli et al. (21), using the Car-Parrinello molecular dynamics with DFT, showed that the electronic band-gap is about 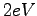$2eV$ and that the first order correction due to the quantistic effects on ions is about 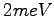$2meV$ for pressure up to $200GPa$ .
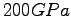Although there are techniques, as Path Integral Monte Carlo, to treat finite temperature quantum systems, they become extremely inefficient for low temperature regime, therefore we have preferred to simply neglect quantum effects due to the finite protons mass.