Quantum Monte Carlo on extended systems

A naive and certainly very inefficient way to study extended system is to simulate clusters of atoms and to investigate the property of the cluster as the number of atoms increase. In this limit the collective behaviour should asymptotically approach to the bulk solid one. However the number of atoms that can be simulated by QMC is so small that the properties of the cluster will be dominated by the surface effects.

Figure 4.1: A simulation box with periodic boundary conditions.

An alternative and efficient way to approximate the bulk properties of an infinite system is the use of periodic boundary conditions (PBC) on a finite box. These boundary conditions mean that the simulation cell is wrapped onto itself and, as an electron moves out of one side of the super-cell it immediately moves back through the opposite side (see figure 4.1). The advantage of using such boundary conditions is that there are no longer "surface electrons" and hence no surface effects. However even with PBC size effects are still present. This is due to the lack of long wavelength fluctuations in the charge density. For a simulation box of linear dimension 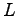$L$ , the periodicity will remove any correlation length greater than $L$ .
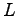In this thesis we used a cubic simulation cell with volume 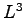$L^3$ with PBC, and the size effects are partially taken into account by increasing the size of the super-cell.
The general hydrogen Hamiltonian with periodic boundary condition is written as:

$$\hat{H} = \sum_{i=1}^N -\frac{1}{2} \nabla^2_i + \frac{1}{2} \sum_{\vec r_i... ...i}^N \sum_{j}^{N_{ions}} \frac{1}{\vert\vec{r}_i - \vec{R}_j - \vec{R}_s \vert}$$

$$+ \frac{1}{2} \sum_{\vec R_i\neq \vec R_j +\vec R_s,\vec R_s} \frac{1}{\vert\vec{R}_i - \vec{R}_j - \vec{R}_s \vert}$$ (4.1)

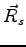where $\vec{R}_s$ are the vectors of the periodic lattice associated with the simulation box, 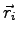$\vec r_i$ are electron coordinates and 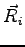$\vec R_i$ are the proton coordinates, and 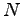$N$ is the number of electrons in the simulation cell. Infinite mass of the protons is assumed so that the kinetic term contains only the electronic contribution. Notice that the Hamiltonian 4.1 is invariant under the translation of any electron coordinate by a vector in 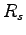${R_s}$ . Moreover if the one body potential is generated by a ionic lattice, the Hamiltonian 4.1 has to be invariant also with respect to a translation given by a vector of the ionic lattice. Notice that only for neutral systems the sum of the one and the two body potential 4.1 is well defined and convergent.