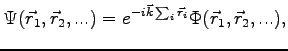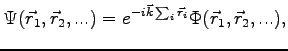Next: Periodic orbitals
Up: Quantum Monte Carlo on
Previous: Quantum Monte Carlo on
Contents
As far as the electron part is concerned, by applying the Bloch's theorem one finds that the eigen-functions for the Hamiltonian 4.1 can be written as:
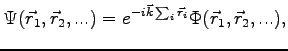 |
(4.2) |
where
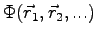 is a function invariant for translation of any electron coordinates by a vector
is a function invariant for translation of any electron coordinates by a vector 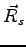 , and
, and 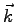 is a vector in the first Brillouin Zone. Although better choices are possible, as Baldereschi's points, or using Twisted Boundary Conditions (76), in this preliminary work on solids we adopted the simplest choice
is a vector in the first Brillouin Zone. Although better choices are possible, as Baldereschi's points, or using Twisted Boundary Conditions (76), in this preliminary work on solids we adopted the simplest choice 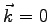 . The correct thermodynamic limit, within the Bohr-Oppenaimer approximation, can be obviously reached for
. The correct thermodynamic limit, within the Bohr-Oppenaimer approximation, can be obviously reached for
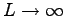 at fixed density
at fixed density
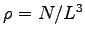 .
In our simulations the distances are evaluated from the
closest image of a given particle. One has to choose carefully an appropriate wave-function for a periodic system. In fact, as the minimal inter-particle distance switches from one image to another, there could be a discontinuity in the derivatives of the wave function.
If this happen, the VMC energy can become lower than the true ground state one. This is due to the fact that the discontinuity leads to
.
In our simulations the distances are evaluated from the
closest image of a given particle. One has to choose carefully an appropriate wave-function for a periodic system. In fact, as the minimal inter-particle distance switches from one image to another, there could be a discontinuity in the derivatives of the wave function.
If this happen, the VMC energy can become lower than the true ground state one. This is due to the fact that the discontinuity leads to 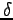 functions that produce a finite positive contribution to the kinetic energy that however will be missed by the VMC sampling procedure, because it occurs in an irrelevant surface of the configuration space.
In the past this problem has been solved by making use of different approaches: either by summing over all possible images by the Ewald sums or by requiring that the trial-function and its derivatives vanish at the surface of the sphere
inscribed within the Wigner-Seitz cell (77).
Instead in the present thesis we introduced a simple and more efficient approach by using periodic orbitals with the correct behavior at
functions that produce a finite positive contribution to the kinetic energy that however will be missed by the VMC sampling procedure, because it occurs in an irrelevant surface of the configuration space.
In the past this problem has been solved by making use of different approaches: either by summing over all possible images by the Ewald sums or by requiring that the trial-function and its derivatives vanish at the surface of the sphere
inscribed within the Wigner-Seitz cell (77).
Instead in the present thesis we introduced a simple and more efficient approach by using periodic orbitals with the correct behavior at 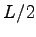 without resorting the expensive evaluation of the Ewald sums.
without resorting the expensive evaluation of the Ewald sums.
Subsections




Next: Periodic orbitals
Up: Quantum Monte Carlo on
Previous: Quantum Monte Carlo on
Contents
Claudio Attaccalite
2005-11-07