



Next: Forces with finite variance
Up: Coulomb Interactions in periodic
Previous: Coulomb Interactions in periodic
Contents
In 1921 Ewald (79) proposed an efficient way to recast the summation 4.9 in two rapidly converging series.
Here in order to derive in a systematic and controlled way the final
result we consider a Yukawa potential
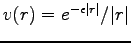 and take the limit
and take the limit
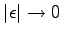 only in the final expression.
Following the Ewald's idea we split the potential in two parts:
only in the final expression.
Following the Ewald's idea we split the potential in two parts:
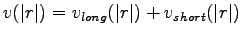 |
(4.10) |
where
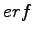 is the error function and
is the error function and 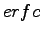 the complementary one.
Notice that the long range part has several important properties:
the complementary one.
Notice that the long range part has several important properties:
On the other hand the short range potential decays very fast in real space
and the sum converges very quickly. Since 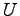 in Eq.(4.9)
depends linearly on the potential, we can easily decompose two contributions:
a short-range and a long range one. Then the latter can be more easily
evaluated in Fourier space:
in Eq.(4.9)
depends linearly on the potential, we can easily decompose two contributions:
a short-range and a long range one. Then the latter can be more easily
evaluated in Fourier space:
where 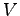 is the volume of the unit cell and the sum over the momenta
are on the discrete
is the volume of the unit cell and the sum over the momenta
are on the discrete 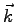 values allowed by the periodicity
values allowed by the periodicity
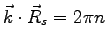 .
In the latter expression we have used Eq.(4.15) and the fact that
the charge neutrality
.
In the latter expression we have used Eq.(4.15) and the fact that
the charge neutrality
 implies that the
implies that the 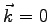 term can be
omitted in the sum for any
term can be
omitted in the sum for any
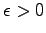 . In this way the limit
. In this way the limit
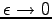 can be found consistently also for long range potentials by replacing expression
(4.14) in the corresponding Fourier transform for
can be found consistently also for long range potentials by replacing expression
(4.14) in the corresponding Fourier transform for 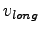 .
For a non neutral system instead the Ewald sum is divergent as expected.
.
For a non neutral system instead the Ewald sum is divergent as expected.
For Coulomb interaction the potential energy becomes:
In the potential energy 4.16
the parameters 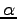 determines the convergence speed in the real and Fourier space series.
For a given choice of
determines the convergence speed in the real and Fourier space series.
For a given choice of 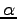 we have chosen a real-space cutoff distance
we have chosen a real-space cutoff distance 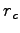 and a
and a 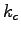 cutoff in the Fourier space. The cutoff
cutoff in the Fourier space. The cutoff 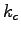 determines the total number of Fourier components,
determines the total number of Fourier components,
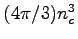 , where
, where 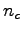 is a positive integer. This parameter has been choosen in such a way that the error on the Ewald summation is much smaller than the Quantum Monte Carlo statistical one.
is a positive integer. This parameter has been choosen in such a way that the error on the Ewald summation is much smaller than the Quantum Monte Carlo statistical one.
A careful choice of the parameter 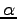 can minimize the error in the summation (see Ref. (80)). In our simulation we have chosen
can minimize the error in the summation (see Ref. (80)). In our simulation we have chosen
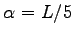 , where
, where 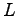 is the size of the simulation box. With this cutoff it is sufficient to sum the short range part in the eq. 4.16 only on the first image of each particle.
Notice that during each VMC or DMC simulation the ionic coordinates are fixed throughout the calculation. Therefore the contribution of the ion-ion Coulomb interaction in the short-range part can be evaluated only at the beginning of the simulation. As an electron
is the size of the simulation box. With this cutoff it is sufficient to sum the short range part in the eq. 4.16 only on the first image of each particle.
Notice that during each VMC or DMC simulation the ionic coordinates are fixed throughout the calculation. Therefore the contribution of the ion-ion Coulomb interaction in the short-range part can be evaluated only at the beginning of the simulation. As an electron 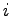 is moved during a VMC calculation the sum of the short range part of the eq. 4.16 is easily updated subtracting the old contribution electron-electron and electron-ion due to the electron
is moved during a VMC calculation the sum of the short range part of the eq. 4.16 is easily updated subtracting the old contribution electron-electron and electron-ion due to the electron 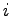 , and adding the new one.
, and adding the new one.
The sum in Fourier space can be written as:
![$\displaystyle U_k = \sum_{ \vec k \neq 0} { \frac{4 \pi }{V \vert\vec k\vert^2}...
...r_i) \right)^2 + \left ( \sum_i^N \cos ( \vec k \vec r_i) \right)^2 \right ] },$](img464.png) |
(4.17) |
then for each 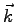 vector all
vector all 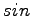 and
and 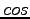 are stored in such a way that when an electron moves, the sum can be easily updated without calculating all the elements from scratch.
are stored in such a way that when an electron moves, the sum can be easily updated without calculating all the elements from scratch.
It is easy to understand that the Ewald summation scales as 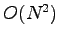 . In fact the updating of the eq. 4.16 costs
. In fact the updating of the eq. 4.16 costs 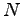 times the number of Fourier's components. Then the number of Fourier component goes as
times the number of Fourier's components. Then the number of Fourier component goes as
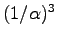 where
where 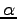 is proportional
is proportional 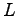 and for a given density scales as
and for a given density scales as 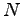 . The Ewald sums are faster than the QMC sweep and so, even if nowadays other faster techniques exist, as for instance particle-mesh-based one, it was not necessary to adopt other more complicated methods in our calculation.
. The Ewald sums are faster than the QMC sweep and so, even if nowadays other faster techniques exist, as for instance particle-mesh-based one, it was not necessary to adopt other more complicated methods in our calculation.




Next: Forces with finite variance
Up: Coulomb Interactions in periodic
Previous: Coulomb Interactions in periodic
Contents
Claudio Attaccalite
2005-11-07
![]() in Eq.(4.9)
depends linearly on the potential, we can easily decompose two contributions:
a short-range and a long range one. Then the latter can be more easily
evaluated in Fourier space:
in Eq.(4.9)
depends linearly on the potential, we can easily decompose two contributions:
a short-range and a long range one. Then the latter can be more easily
evaluated in Fourier space:
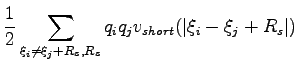
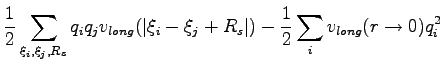
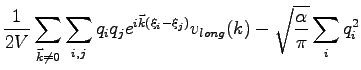
![]() determines the convergence speed in the real and Fourier space series.
For a given choice of
determines the convergence speed in the real and Fourier space series.
For a given choice of ![]() we have chosen a real-space cutoff distance
we have chosen a real-space cutoff distance ![]() and a
and a ![]() cutoff in the Fourier space. The cutoff
cutoff in the Fourier space. The cutoff ![]() determines the total number of Fourier components,
determines the total number of Fourier components,
![]() , where
, where ![]() is a positive integer. This parameter has been choosen in such a way that the error on the Ewald summation is much smaller than the Quantum Monte Carlo statistical one.
is a positive integer. This parameter has been choosen in such a way that the error on the Ewald summation is much smaller than the Quantum Monte Carlo statistical one.
![]() can minimize the error in the summation (see Ref. (80)). In our simulation we have chosen
can minimize the error in the summation (see Ref. (80)). In our simulation we have chosen
![]() , where
, where ![]() is the size of the simulation box. With this cutoff it is sufficient to sum the short range part in the eq. 4.16 only on the first image of each particle.
Notice that during each VMC or DMC simulation the ionic coordinates are fixed throughout the calculation. Therefore the contribution of the ion-ion Coulomb interaction in the short-range part can be evaluated only at the beginning of the simulation. As an electron
is the size of the simulation box. With this cutoff it is sufficient to sum the short range part in the eq. 4.16 only on the first image of each particle.
Notice that during each VMC or DMC simulation the ionic coordinates are fixed throughout the calculation. Therefore the contribution of the ion-ion Coulomb interaction in the short-range part can be evaluated only at the beginning of the simulation. As an electron ![]() is moved during a VMC calculation the sum of the short range part of the eq. 4.16 is easily updated subtracting the old contribution electron-electron and electron-ion due to the electron
is moved during a VMC calculation the sum of the short range part of the eq. 4.16 is easily updated subtracting the old contribution electron-electron and electron-ion due to the electron ![]() , and adding the new one.
, and adding the new one.