



Next: Introduction
Up: thesis
Previous: List of Tables
Contents
- Example of the convergence of the SR method for the
variational parameters as a function of the
number of stochastic iterations. In the upper(lower) panel
the Jastrow (geminal) parameters are shown.
For each iteration, a variational Monte Carlo
calculation is employed with a bin containing
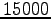 samples of the energy, yielding at the equilibrium
a standard deviation of
samples of the energy, yielding at the equilibrium
a standard deviation of
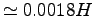 .
For the first 200 iteration
.
For the first 200 iteration
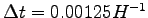 ,
for the further 200 iterations
,
for the further 200 iterations
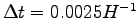 ,
whereas for the remaining ones
,
whereas for the remaining ones
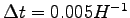 .
.
- Calculation of the derivative of the energy with respect to the
second
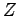 in the
in the 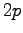 orbital of the geminal function for the Be atom.
The calculation of the force was obtained, at fixed variational
parameters, by averaging over
orbital of the geminal function for the Be atom.
The calculation of the force was obtained, at fixed variational
parameters, by averaging over 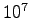 samples, allowing e.g. a statistical accuracy in the total energy of
samples, allowing e.g. a statistical accuracy in the total energy of
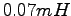 . The variational parameters have been obtained by
an SR minimization with fixed bin length shown in the x label.
The parameter considered has
the largest deviation from the Euler conditions.
. The variational parameters have been obtained by
an SR minimization with fixed bin length shown in the x label.
The parameter considered has
the largest deviation from the Euler conditions.
- Plot of the equilibrium distance of the
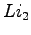 molecule as a function
of the inverse bin length. The total energy and
the binding energy are reported in Tables 3.3 and 3.2
respectively.
For all simulations the
initial wave-function is optimized at
molecule as a function
of the inverse bin length. The total energy and
the binding energy are reported in Tables 3.3 and 3.2
respectively.
For all simulations the
initial wave-function is optimized at 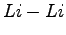 distance
distance 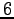 a.u.
a.u.
- Electron density (atomic units) projected on the plane of
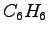 . The surface plot
shows the difference between the resonating valence bond wave function, with the correct
. The surface plot
shows the difference between the resonating valence bond wave function, with the correct
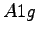 symmetry of the molecule, and a non-resonating one, which has the symmetry of the Hartree Fock wave function.
symmetry of the molecule, and a non-resonating one, which has the symmetry of the Hartree Fock wave function.
- Surface plot of the charge
density projected onto the molecular plane.
The difference between the non-resonating
(indicated as HF) and resonating Kekulé 3-body Jastrow wave function
densities is shown.
Notice the corresponding change
from a dimerized structure to a
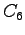 rotational invariant density
profile.
rotational invariant density
profile.
- Plot of the convergence toward the equilibrium geometry for the
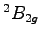 acute and the
acute and the 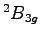 obtuse benzene cation. Notice that both the
simulations start form the ground state neutral benzene geometry and relax
with a change both in the
obtuse benzene cation. Notice that both the
simulations start form the ground state neutral benzene geometry and relax
with a change both in the 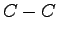 bond lengths and in the angles. The symbols
are the same of Tab. 3.5.
bond lengths and in the angles. The symbols
are the same of Tab. 3.5.
- A simulation box with periodic boundary conditions.
- Ionic dynamics of 54 hydrogen atoms using GLQ, with a time step
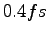 , starting from a BCC lattice. The trial wave-function contains 2920 variational parameters and we have optimized 300 of them at each step. In the inset the maximum deviation
, starting from a BCC lattice. The trial wave-function contains 2920 variational parameters and we have optimized 300 of them at each step. In the inset the maximum deviation
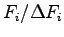 of the forces acting on the variational parameters is shown.
of the forces acting on the variational parameters is shown.
- Energy per atom of 16 hydrogen atoms at Rs=1.31 calculated on configurations obtained by CEIMC with the method (8). The first 10 configurations are in the atomic liquid phase at 2000k while in the last ten the system is forming clusters at T=500.
- Variance per atom of 16 hydrogen atoms at Rs=1.31 calculated on configuration obtained by CEIMC with the method (8). The first 10 configurations are in the atomic liquid phase at 2000k while in the last ten the system is forming clusters at T=500.
- Proton-proton correlation function, g(r), at Rs=1.31. The GLQ and CEIMC have used a periodical simulation box with 32 atoms while Hohl et al. with 64 atoms. All the calculations were performed for a single
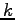 point (
point (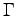 ).
).
- Comparison of the proton-proton correlation function, g(r), at Rs=2.1 and T=4350 obtained with different methods CEIMC (8) (7) and GLQ. All the simulations were performed with 32 atoms for a single
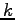 point (
point (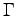 ).
).
- Variational and Diffusion Condensation Energy per atom
- Eigenvalues of the
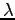 matrix for 16 hydrogen atoms at Rs=1.31 and 100K as function of the simulation time
matrix for 16 hydrogen atoms at Rs=1.31 and 100K as function of the simulation time
- Off-Diagonal Long Range Order for 16 hydrogen atoms at Rs=1.31 and 100K, in a box of size
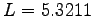 , for
, for 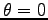 as function of the distance
as function of the distance 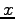
- Off-Diagonal Long Range Order for 54 hydrogen atoms at Rs=1.31 at 100K in a box of size
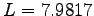 , for
, for 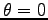 as function of the distance
as function of the distance 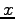
Claudio Attaccalite
2005-11-07