Introduction

There is an oral tradition that says shortly after the Shrödinger equation was validated on 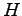$H$ atom and 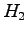$H_2$ P.A.M. Dirac exclaimed that the chemistry had come to an end. Fortunately some years later, in 1929, he added "The fundamental laws necessary for the mathematical treatment of a large part of physics and the whole of chemistry are thus completely known, and the difficulty lies only in the fact that application of these laws leads to equations that are too complex to be solved.".
During the last 70 years, staring from the Thomas-Fermi theory, there were proposed many ways to solve approximately the Shrödinger equation with several electrons. In 1999 W. Kohn and J.Sham received the Nobel prize for the well known Densitiy Functional Theory. They found an innovative way to deal with many electron system using a three-dimensional electronic density instead of a 3N-dimension wave-function. Their approach have opened the possibility to simulate thousands of different systems with an affordable computer effort.
Several other techniques, different from DFT, exist to deal with the time-independent Shrödinger equation with many electrons. The so colled Quantum Monte Carlo (QMC) techniques (10,11,9) are some of the most accurate and efficient statistical methods for treating many body quantum systems. In the past they were used to study different systems as quantum liquids (12,13,14), atoms (2), molecules (16,15), solids (17) and lattice models for strongly correlated electron systems (18). Moreover QMC allows to include many important physical informations of the system, such as cusp conditions, symmetries, exact limits, because it deals directly with the many body wave-function. In this thesis we have used these techniques to study molecular systems by introducing a new highly correlated wave-function (19).
Although QMC have led to great progress in understanding the zero temperature physics of strongly correlated electron systems, there is no obvious way to extend it to finite low temperature. Even if there exist Monte Carlo techniques, as Path Integral Monte Carlo, to study quantum system at finite temperature, they are limited to the high temperature regime.
In this thesis following the idea of Car and Parrinello we present a new approach to study many electron systems at low temperature using a classical ionic dynamic combined with a ground state QMC for the electrons. This method is then applied to study high pressure hydrogen.
Hydrogen is the most abundant element in the universe. Despite the simple structure of hydrogen atom, it does not form the simplest solids or liquids. It has a very complex phase diagram that has been widely studied by experimental (20) and theoretical approaches (8,21).
At low pressure hydrogen crystallizes as an insulating molecular solid. As the pressure increase different molecular phases were encountered (20,22). At higher pressure electron would no longer remain in localized bound orbitals and would instead delocalize. As predicted by the pioneering work of Wigner and Huntington (1935), at extreme pressure, comparable with the ones present in giant planets, the molecules of solid hydrogen will dissociate to form a mono-atomic metallic solid. Despite the simple interaction, the structure of this solid has been predicted to be a simple hexagonal lattice (23). At higher density some theoretical models has suggested that compressed hydrogen can form unusual two-component quantum fluid, made by electrons and protons, at low and even zero temperature (25,24). Moreover a recent study (21) predicted a maximum in the melting curve between solid and liquid in high pressure hydrogen, confirming the idea of a possible stable quantum fluid phase at low temperature.
Motivated by the so reach phase diagram we decided to investigate the effects of the correlation in high pressure hydrogen, and to this end, we decided to use a resonating valence bond (RVB) wave-function together with a new technique to simulate finite temperature systems. In the RVB approach the variational trial-function is written as an antisymmetrized combination of bonds. Each bond contains two electrons shared by two orbitals. In fact after the original proposal by Anderson, there is now a large amount of numerical evidence that the simple but general resonating valence bond (RVB) wave function contains just those ingredients missing in uncorrelated theories, so that the main features of electron correlation can be captured by the variational RVB approach. Moreover from the computational point of view the remarkable feature of this approach is that several resonating valence bonds can be dealt simultaneously with a single determinant, at a computational cost growing with the number of electrons similarly to more conventional methods, such as Hartree-Fock or Density Functional Theory.