



Next: Stabilization of the SR
Up: Stochastic Reconfiguration
Previous: Stochastic Reconfiguration
Contents
In this thesis
we have determined 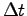 by verifying the stability and the convergence of the SR algorithm for fixed
by verifying the stability and the convergence of the SR algorithm for fixed 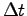 value.
value.
The simulation is stable whenever
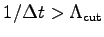 ,
where
,
where
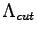 is an energy cutoff that is strongly
dependent on the chosen wave function
and it is generally weakly dependent on the bin length.
Whenever the wave function is too much detailed, namely has a lot of variational freedom,
especially for the high energy components of the core electrons,
the value of
is an energy cutoff that is strongly
dependent on the chosen wave function
and it is generally weakly dependent on the bin length.
Whenever the wave function is too much detailed, namely has a lot of variational freedom,
especially for the high energy components of the core electrons,
the value of
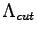 becomes exceedingly large
and too many iterations are required for obtaining a
converged variational wave function.
In fact a rough estimate of the
corresponding number of iterations
becomes exceedingly large
and too many iterations are required for obtaining a
converged variational wave function.
In fact a rough estimate of the
corresponding number of iterations 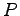 is given by
is given by
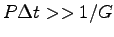 , where
, where 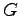 is the typical energy gap
of the system, of the order of few electron Volts
in small atoms and molecules.
Within the SR method it is therefore extremely important to work with a
bin length rather small, so that many iterations can be performed without
much effort.
is the typical energy gap
of the system, of the order of few electron Volts
in small atoms and molecules.
Within the SR method it is therefore extremely important to work with a
bin length rather small, so that many iterations can be performed without
much effort.
Figure 2.1:
Example of the convergence of the SR method for the
variational parameters as a function of the
number of stochastic iterations. In the upper(lower) panel
the Jastrow (geminal) parameters are shown.
For each iteration, a variational Monte Carlo
calculation is employed with a bin containing 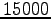 samples of the energy, yielding at the equilibrium
a standard deviation of
samples of the energy, yielding at the equilibrium
a standard deviation of
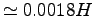 .
For the first 200 iteration
.
For the first 200 iteration
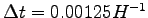 ,
for the further 200 iterations
,
for the further 200 iterations
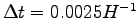 ,
whereas for the remaining ones
,
whereas for the remaining ones
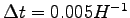 .
.
![\includegraphics[width=\textwidth,height=12cm]{parameters.eps}](img206.png) |
In a Monte Carlo optimization framework the forces 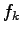 are always determined
with some statistical noise
are always determined
with some statistical noise 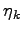 , and by iterating
the procedure several times with a fixed bin length
the variational parameters will fluctuate around their mean
values. These statistical fluctuations are similar to the
thermal noise of a standard Langevin equation:
, and by iterating
the procedure several times with a fixed bin length
the variational parameters will fluctuate around their mean
values. These statistical fluctuations are similar to the
thermal noise of a standard Langevin equation:
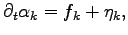 |
(2.14) |
where
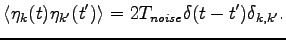 |
(2.15) |
The variational parameters 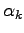 , averaged over the
Langevin simulation time (as for instance in Fig.2.1), will be close to the true energy minimum,
but the corresponding forces
, averaged over the
Langevin simulation time (as for instance in Fig.2.1), will be close to the true energy minimum,
but the corresponding forces
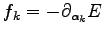 will be
affected by a bias that scales to zero with the thermal noise
will be
affected by a bias that scales to zero with the thermal noise 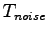 .
Within a QMC scheme, one needs to estimate
.
Within a QMC scheme, one needs to estimate 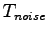 by increasing the bin length, as clearly
by increasing the bin length, as clearly
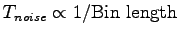 , this noise being
directly related to the statistical fluctuations of the forces.
Thus there is an optimal value for the bin length, which guarantees a fast
convergence and avoid the forces to be biased within the statistical accuracy
of the sampling. Moreover in the fluctuation around the minimum also non Gaussian correction will be present, but in analogy to the an-harmonic effects in solids, this error is expected to vanish linearly with the temperature
, this noise being
directly related to the statistical fluctuations of the forces.
Thus there is an optimal value for the bin length, which guarantees a fast
convergence and avoid the forces to be biased within the statistical accuracy
of the sampling. Moreover in the fluctuation around the minimum also non Gaussian correction will be present, but in analogy to the an-harmonic effects in solids, this error is expected to vanish linearly with the temperature 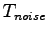 .
An example is shown in Fig. 2.1 for the
optimization of the Be atom, using a basis two exponentials for each orbital both for the geminal
and the three-body Jastrow part. The convergence is reached in about
1000 iteration with
.
An example is shown in Fig. 2.1 for the
optimization of the Be atom, using a basis two exponentials for each orbital both for the geminal
and the three-body Jastrow part. The convergence is reached in about
1000 iteration with
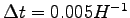 . However, in this case
it is possible to use a small bin length,
yielding a statistical accuracy in the energy much poorer than the
final accuracy of about
. However, in this case
it is possible to use a small bin length,
yielding a statistical accuracy in the energy much poorer than the
final accuracy of about 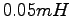 .
This is obtained
by averaging the variational
parameters in the last
.
This is obtained
by averaging the variational
parameters in the last 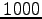 iterations,
when they fluctuate around a mean value, allowing
a very accurate determination of the energy minimum which
satisfies the Euler conditions, namely with
iterations,
when they fluctuate around a mean value, allowing
a very accurate determination of the energy minimum which
satisfies the Euler conditions, namely with 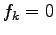 for all parameters.
Those conditions have been tested
by an independent
Monte Carlo simulation about
for all parameters.
Those conditions have been tested
by an independent
Monte Carlo simulation about 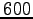 times longer than the bin used
during the minimization.
times longer than the bin used
during the minimization.
Figure 2.2:
Calculation of the derivative of the energy with respect to the
second 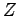 in the
in the 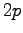 orbital of the geminal function for the Be atom.
The calculation of the force was obtained, at fixed variational
parameters, by averaging over
orbital of the geminal function for the Be atom.
The calculation of the force was obtained, at fixed variational
parameters, by averaging over 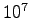 samples, allowing e.g. a statistical accuracy in the total energy of
samples, allowing e.g. a statistical accuracy in the total energy of
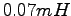 . The variational parameters have been obtained by
an SR minimization with fixed bin length shown in the x label.
The parameter considered has
the largest deviation from the Euler conditions.
. The variational parameters have been obtained by
an SR minimization with fixed bin length shown in the x label.
The parameter considered has
the largest deviation from the Euler conditions.
![\includegraphics[width=\textwidth]{forzap19.eps}](img218.png) |
As shown in Fig. 2.2
the Euler conditions are fulfilled within statistical accuracy
even when the bin used for the minimization is much smaller than the
overall simulation. On the other hand if the bin used is too small,
as we have already pointed out, the averaging of the parameters is
affected by a sizable bias.
Whenever it is possible to use a relatively small bin
in the minimization, the apparently large
number of iterations required for equilibration does not really matter,
because a comparable amount of time has to be spent in the averaging
of the variational parameters, as shown in Fig. 2.1.
It is easy to convince oneself that for high enough accuracy the number
of iterations needed for the equilibration becomes negligible
from the computational point of view. In fact, in order to reduce, e.g.
by a factor of ten, the accuracy in the variational parameters, a bin
ten times larger is required
for decreasing the thermal noise 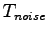 by the same factor. Whereas to reduce the statistical errors by the same ratio, it has to be done average on
by the same factor. Whereas to reduce the statistical errors by the same ratio, it has to be done average on 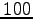 times steps more.
This means that the fraction of
time spent for equilibration
becomes ten times smaller compared with the less accurate simulation.
times steps more.
This means that the fraction of
time spent for equilibration
becomes ten times smaller compared with the less accurate simulation.




Next: Stabilization of the SR
Up: Stochastic Reconfiguration
Previous: Stochastic Reconfiguration
Contents
Claudio Attaccalite
2005-11-07
![]() ,
where
,
where
![]() is an energy cutoff that is strongly
dependent on the chosen wave function
and it is generally weakly dependent on the bin length.
Whenever the wave function is too much detailed, namely has a lot of variational freedom,
especially for the high energy components of the core electrons,
the value of
is an energy cutoff that is strongly
dependent on the chosen wave function
and it is generally weakly dependent on the bin length.
Whenever the wave function is too much detailed, namely has a lot of variational freedom,
especially for the high energy components of the core electrons,
the value of
![]() becomes exceedingly large
and too many iterations are required for obtaining a
converged variational wave function.
In fact a rough estimate of the
corresponding number of iterations
becomes exceedingly large
and too many iterations are required for obtaining a
converged variational wave function.
In fact a rough estimate of the
corresponding number of iterations ![]() is given by
is given by
![]() , where
, where ![]() is the typical energy gap
of the system, of the order of few electron Volts
in small atoms and molecules.
Within the SR method it is therefore extremely important to work with a
bin length rather small, so that many iterations can be performed without
much effort.
is the typical energy gap
of the system, of the order of few electron Volts
in small atoms and molecules.
Within the SR method it is therefore extremely important to work with a
bin length rather small, so that many iterations can be performed without
much effort.
![\includegraphics[width=\textwidth,height=12cm]{parameters.eps}](img206.png)
![]() are always determined
with some statistical noise
are always determined
with some statistical noise ![]() , and by iterating
the procedure several times with a fixed bin length
the variational parameters will fluctuate around their mean
values. These statistical fluctuations are similar to the
thermal noise of a standard Langevin equation:
, and by iterating
the procedure several times with a fixed bin length
the variational parameters will fluctuate around their mean
values. These statistical fluctuations are similar to the
thermal noise of a standard Langevin equation:
![\includegraphics[width=\textwidth]{forzap19.eps}](img218.png)
![]() by the same factor. Whereas to reduce the statistical errors by the same ratio, it has to be done average on
by the same factor. Whereas to reduce the statistical errors by the same ratio, it has to be done average on ![]() times steps more.
This means that the fraction of
time spent for equilibration
becomes ten times smaller compared with the less accurate simulation.
times steps more.
This means that the fraction of
time spent for equilibration
becomes ten times smaller compared with the less accurate simulation.