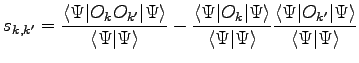 |
(2.16) |
The first successful proposal to control this instability was to remove from
the inversion problem (49), required for the minimization, those
directions in the variational parameter space corresponding to exceedingly
small eigenvalues ![]() .
In this thesis we describe a method the is much better.
As a first step, we show that the reason of the
large condition number
.
In this thesis we describe a method the is much better.
As a first step, we show that the reason of the
large condition number ![]() is due to the existence of ''redundant''
variational parameters that do not make changes to the wave function
within a prescribed tolerance
is due to the existence of ''redundant''
variational parameters that do not make changes to the wave function
within a prescribed tolerance ![]() .
.
Indeed in practical calculations, we are interested in the minimization
of the wave function within a reasonable accuracy.
The tolerance ![]() may represent therefore the distance
between the exact normalized variational wave function which
minimizes the energy expectation value and the
approximate acceptable one,
for which we no longer iterate the minimization
scheme. For instance
may represent therefore the distance
between the exact normalized variational wave function which
minimizes the energy expectation value and the
approximate acceptable one,
for which we no longer iterate the minimization
scheme. For instance
![]() is by far acceptable for
chemical and physical interest.
is by far acceptable for
chemical and physical interest.
A stable algorithm is then obtained by simply
removing the parameters that do not change the wave function
by less than ![]() from the minimization.
An efficient scheme to remove the ''redundant parameters'' is also given.
from the minimization.
An efficient scheme to remove the ''redundant parameters'' is also given.
Let us consider the ![]() normalized states orthogonal
to
normalized states orthogonal
to ![]() , but not mutually orthogonal:
, but not mutually orthogonal:
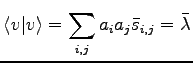 |
(2.20) |
In general whenever there
are ![]() vectors
vectors ![]() that are below the tolerance
that are below the tolerance ![]() the optimal choice to stabilize the minimization procedure is
to remove
the optimal choice to stabilize the minimization procedure is
to remove ![]() rows and
rows and ![]() columns from the matrix (2.18),
in such a way that the corresponding determinant of the
columns from the matrix (2.18),
in such a way that the corresponding determinant of the
![]() overlap matrix is maximum.
overlap matrix is maximum.
From practical purposes it is enough to consider an iterative scheme
to find a large minor, but not necessarily the maximum one.
This method is based on the inverse of ![]() . At each step we remove the
. At each step we remove the
![]() row and column from
row and column from ![]() for which
for which
![]() is
maximum. We stop to remove rows and columns after
is
maximum. We stop to remove rows and columns after ![]() inversions.
In this approach we exploit the fact that, by a consequence of
the Laplace theorem on determinants,
inversions.
In this approach we exploit the fact that, by a consequence of
the Laplace theorem on determinants,
![]() is the ratio between the described minor without
the
is the ratio between the described minor without
the ![]() row and column and the determinant of the full
row and column and the determinant of the full
![]() matrix.
Since within a stochastic method it is certainly not possible to work with a
machine precision tolerance, setting
matrix.
Since within a stochastic method it is certainly not possible to work with a
machine precision tolerance, setting
![]() guarantees a stable algorithm, without affecting
the accuracy of the calculation.
The advantage of this scheme, compared with the previous one(18),
is that the less relevant parameters can be easily identified
after few iterations and do not change further in the process of minimization.
guarantees a stable algorithm, without affecting
the accuracy of the calculation.
The advantage of this scheme, compared with the previous one(18),
is that the less relevant parameters can be easily identified
after few iterations and do not change further in the process of minimization.