



Next: List of Figures
Up: thesis
Previous: Contents
Contents
- Total energies in variational (
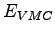 ) and
diffusion (
) and
diffusion (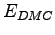 ) Monte Carlo calculations;
the percentages of correlation energy recovered in
VMC (
) Monte Carlo calculations;
the percentages of correlation energy recovered in
VMC (
 ) and DMC (
) and DMC (
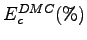 ) have been evaluated using
the ``exact'' (
) have been evaluated using
the ``exact'' (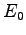 ) and Hartree-Fock (
) and Hartree-Fock (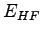 ) energies from
the references (1). Here ``exact'' means the ground state
energy of the non relativistic infinite nuclear mass Hamiltonian.
The energies are in Hartree.
) energies from
the references (1). Here ``exact'' means the ground state
energy of the non relativistic infinite nuclear mass Hamiltonian.
The energies are in Hartree.
- Bond lengths (
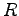 ) in atomic units;
the subscript 0
refers to the ``exact'' results.
For the water molecule
) in atomic units;
the subscript 0
refers to the ``exact'' results.
For the water molecule 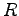 is the distance between O and H
and
is the distance between O and H
and 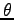 is the angle HOH (in deg), for
is the angle HOH (in deg), for 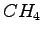
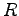 is the distance between
C and H and
is the distance between
C and H and 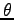 is the HCH angle.
is the HCH angle.
- Binding energies in
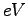 obtained by variational (
obtained by variational (
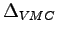 ) and diffusion
(
) and diffusion
(
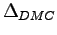 ) Monte Carlo calculations;
) Monte Carlo calculations;
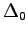 is the ``exact'' result for the non-relativistic infinite nuclear
mass Hamiltonian.
Also the percentages (
is the ``exact'' result for the non-relativistic infinite nuclear
mass Hamiltonian.
Also the percentages (
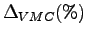 and
and
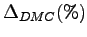 )
of the total binding energies are reported.
)
of the total binding energies are reported.
- Binding energies in
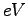 obtained by variational (
obtained by variational (
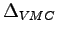 ) and diffusion
(
) and diffusion
(
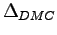 ) Monte Carlo calculations with different trial wave functions
for benzene. In order to calculate the binding energies yielded
by the 2-body Jastrow we used the atomic energies reported
in Ref. (2).
The percentages (
) Monte Carlo calculations with different trial wave functions
for benzene. In order to calculate the binding energies yielded
by the 2-body Jastrow we used the atomic energies reported
in Ref. (2).
The percentages (
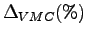 and
and
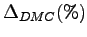 )
of the total binding energies are also reported.
)
of the total binding energies are also reported.
- Bond lengths (
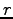 ) for the two lowest
) for the two lowest 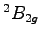 and
and 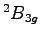 states of the benzene radical cation. The angles
states of the benzene radical cation. The angles 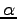 are expressed
in degrees, the lengths in
are expressed
in degrees, the lengths in 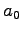 . The carbon sites are numerated from 1 to 6.
. The carbon sites are numerated from 1 to 6.
- Total energies for the
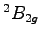 and
and 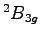 states of the benzene radical cation
after the geometry relaxation. A comparison with a BLYP/6-31G* and
SVWN/6-31G* all-electron
calculation (Ref. (3)) is reported.
states of the benzene radical cation
after the geometry relaxation. A comparison with a BLYP/6-31G* and
SVWN/6-31G* all-electron
calculation (Ref. (3)) is reported.
- Adiabatic ionization potential of the benzene molecule;
our estimate is done for the
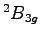 relaxed geometries
of the benzene radical cation, with an inclusion of the zero point motion
correction between the
relaxed geometries
of the benzene radical cation, with an inclusion of the zero point motion
correction between the 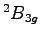 state and the
state and the 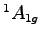 neutral molecule
ground state, calculated in Ref. (4) at the B3LYP/6-31G*
level.
neutral molecule
ground state, calculated in Ref. (4) at the B3LYP/6-31G*
level.
- Total energies in variational (
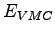 ) and
diffusion (
) and
diffusion (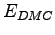 ) Monte Carlo calculations for 16 hydrogen atoms in a BCC lattice
at Rs=1.31 and T=0 (i.e. frozen ion positions). The energies are in Hartree for atom.
) Monte Carlo calculations for 16 hydrogen atoms in a BCC lattice
at Rs=1.31 and T=0 (i.e. frozen ion positions). The energies are in Hartree for atom.
- Pressure at different temperatures and densities. We report also the pressure obtained with Gasgun experiment (5), with Silvera-Goldman empirical potential model (6) and CEICM method (7) at
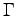 point. The pressure are in GPa.
point. The pressure are in GPa.
Claudio Attaccalite
2005-11-07