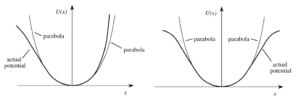
The Lorentz model of the atom, which treats the atom as a harmonic oscillator, is known to provide a very good description of the linear optical properties of atomic vapors and of nonmetallic solids. The model is extended by allowing the possibility of a nonlinearity in the restoring force exerted on the electron. This additional non-linear force may or not break inversion symmetry, see figure below.
Anharmonic oscillator: with broken inversion symmetry (left) and with inversion symmetry (right)
The student should write a Python code that first integrates the standard
harmonic oscillator equation, and compare the result with the analytic solution.
Then he will include the non-linear corrections and compare the response functions with the one calculated in the Boyd book[3] in both the cases the one with or without inversion symmetry.
Reference: