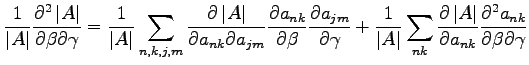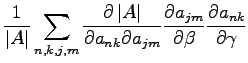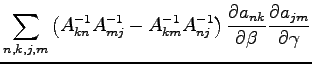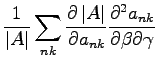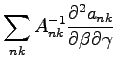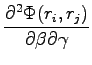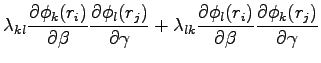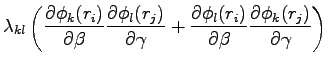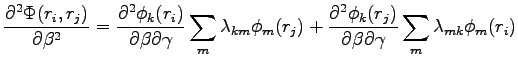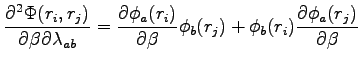Next: Derivatives of the Local
Up: Pairing determinant
Previous: The logarithmic derivatives
Contents
In the general case in which all elements of the matrix depend from the parameters
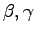 the derivative is:
the derivative is:
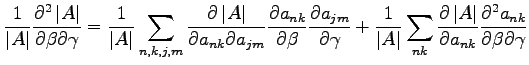 |
(B.17) |
now using equations D.3 and D.5
where the derivatives
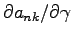 ,
,
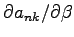 are given by B.15, B.16, B.14.
The second derivatives can be evaluate from B.8.
are given by B.15, B.16, B.14.
The second derivatives can be evaluate from B.8.
If 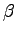 and
and 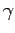 are two
are two
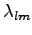 using B.16 the second derivative is obviously zero.
using B.16 the second derivative is obviously zero.
If 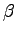 and
and 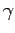 are both orbital parameters, and for example the
are both orbital parameters, and for example the 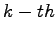 orbital depends from
orbital depends from 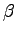 and
and 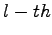 orbital from
orbital from 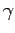 , using B.15 we have:
, using B.15 we have:
because
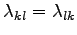 .
.
If 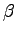 and
and 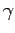 are parameters of the same orbital we have:
are parameters of the same orbital we have:
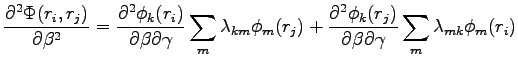 |
(B.21) |
If 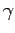 is one of the
is one of the 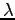 parameter, using the fact the
parameter, using the fact the 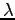 matrix is symmetric we obtain:
matrix is symmetric we obtain:
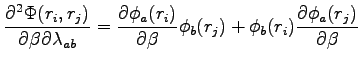 |
(B.22) |




Next: Derivatives of the Local
Up: Pairing determinant
Previous: The logarithmic derivatives
Contents
Claudio Attaccalite
2005-11-07