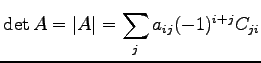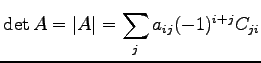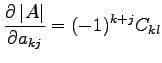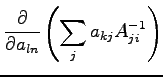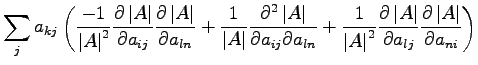Next: Error Analysis due to
Up: thesis
Previous: Cusp conditions
Contents
Determinant derivatives
Consider a matrix 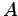 , we want find a simple way to express derivatives of the its determinant respect to the matrix elements
, we want find a simple way to express derivatives of the its determinant respect to the matrix elements 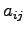 .
The determinant can be expanded in the elements
.
The determinant can be expanded in the elements 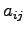 :
:
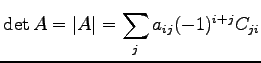 |
(D.1) |
where 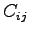 is the minor of the matrix
is the minor of the matrix 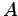 respect to the element
respect to the element 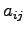 and therefore does not depend explicitly by the elements of the raw
and therefore does not depend explicitly by the elements of the raw 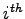 . So the derivative with respect to
. So the derivative with respect to 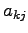 will be:
will be:
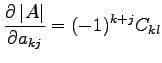 |
(D.2) |
and for the logarithmic derivative we have:
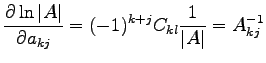 |
(D.3) |
We want to find a simple relation to evaluate second derivatives of the determinant. We write the relation
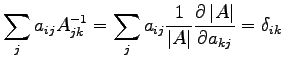 |
(D.4) |
if we derive this equation for  we obtain:
we obtain:
where we substitute the
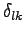 with the eq. D.4. Because of this equation is zero for all
with the eq. D.4. Because of this equation is zero for all 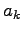 this means that the expression in parentheses is zero, and this yields to:
this means that the expression in parentheses is zero, and this yields to:
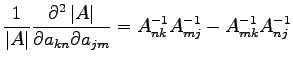 |
(D.5) |




Next: Error Analysis due to
Up: thesis
Previous: Cusp conditions
Contents
Claudio Attaccalite
2005-11-07