



Next: Determinant derivatives
Up: thesis
Previous: Derivatives of the local
Contents
Cusp conditions
When two Coulomb particles get close, the potential has 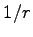 singularity.
We want modify the wave function in such a way to cancel this singularity.
Let us consider the case of an electron close to a nucleus, the Schrödinger equation reduces to:
singularity.
We want modify the wave function in such a way to cancel this singularity.
Let us consider the case of an electron close to a nucleus, the Schrödinger equation reduces to:
![$\displaystyle \left[- \frac{1}{2L^2} \nabla_e^2 - \frac{Ze^2}{rL}\right] \psi = E \psi$](img750.png) |
(C.1) |
where 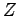 is the nuclear charge, notice that we used rescaled distances (see Eq. 4.23). Writing the first term in spherical coordinates, we get
is the nuclear charge, notice that we used rescaled distances (see Eq. 4.23). Writing the first term in spherical coordinates, we get
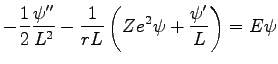 |
(C.2) |
To cancel the singularity at small 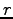 the term multiplying by
the term multiplying by 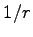 must vanish. So we have
must vanish. So we have
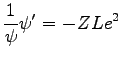 |
(C.3) |
If
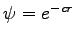 we must have
we must have 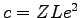 .
For the case of two electrons, when they are close each other the Schrödinger equation, using relative coordinates
.
For the case of two electrons, when they are close each other the Schrödinger equation, using relative coordinates
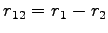 , reduces to
, reduces to
![$\displaystyle \left[- \frac{\nabla_{12}^2}{L^2} + \frac{e^2}{L r_{12}}\right] \psi = E \psi$](img756.png) |
(C.4) |
Electrons with unlike spins have an extra factor of 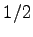 in the cusp condition compared with the electron-nucleus case. So we have
in the cusp condition compared with the electron-nucleus case. So we have
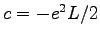 .
In the antisymmetric case, the electrons will be in a relative
.
In the antisymmetric case, the electrons will be in a relative 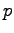 state,
reducing the cusp condition by
state,
reducing the cusp condition by 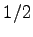 , so
, so
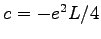 .
Since the antisymmetry requirement keeps them apart anyway having the correct cusp for like spin electrons leads to a very little in the energy or the variance(see Ref. (39).
.
Since the antisymmetry requirement keeps them apart anyway having the correct cusp for like spin electrons leads to a very little in the energy or the variance(see Ref. (39).




Next: Determinant derivatives
Up: thesis
Previous: Derivatives of the local
Contents
Claudio Attaccalite
2005-11-07
![$\displaystyle \left[- \frac{1}{2L^2} \nabla_e^2 - \frac{Ze^2}{rL}\right] \psi = E \psi$](img750.png)
![$\displaystyle \left[- \frac{1}{2L^2} \nabla_e^2 - \frac{Ze^2}{rL}\right] \psi = E \psi$](img750.png)
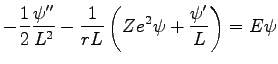
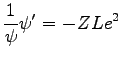
![$\displaystyle \left[- \frac{\nabla_{12}^2}{L^2} + \frac{e^2}{L r_{12}}\right] \psi = E \psi$](img756.png)