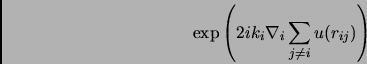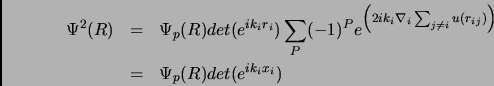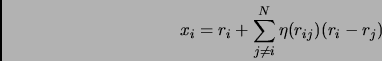I nodi di backflow

E' possibile migliorare la struttura nodale della nostra funzione d'onda inserendo gli effetti di backflow. L'idea del backflow è stato originariamente proposta da Feyman e Cohen [41]; noi ci siamo basati su come è stato utilizzato nel lavoro di Kwon, Ceperley e Martin [42].
Vediamo ora come sia possibile ricavare in modo semplice una forma funzionale che contenga l'effetto del backflow. Per migliorare la nostra funzione d'onda possiamo applicare a quest'ultima l'operatore 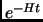$e^{-Ht}$ che proietta una qualsiasi funzione d'onda, non ortogonale allo stato fondamentare, nello stato fondamentale

$$\Psi(R) = \lim_{t \rightarrow \infty}e^{-tH} \Psi(R)^{n}$$

Questa relazione può essere scritta tramite integrali di cammino usando il drifting random walk (DRW) [43] e la funzione proiettata può riscriversi tramite una generalizzazione della formula di Feyman-Kac:

$$\Psi_{n+1}(R) = e^{-H} \Psi_n(R) = \Psi_n(R) \left \langle \exp{ -\int_0^t E_n [ R(t') ]} \right \rangle_{DRW}$$ (3.8)

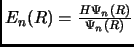Dove $E_n(R)=\frac{H \Psi_n(R)}{\Psi_n(R)}$ è l'energia locale. La media 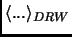$\langle ... \rangle_{DRW}$ è fatta su di un processo diffusivo (drift random walk) definito dall'equazione:

$$-\frac{df(R,t)}{dt} = \lambda \sum_{i=1}^N \nabla \left [ - \nabla f(R,t) - 2 f(R,t) \nabla \ln{(\Psi_n(R))} \right ]$$ (3.9)

Poichè l'Hamiltoniana non tiene conto del fatto che sto trattanto fermioni, questo processo diffusivo mi farebbe evolvere verso lo stato bosonico, devo allora aggiungere un operatore di antisimmetrizzazione. Poiché l'antisimetrizzazione è un'operazione lineare, questa commuterà con l'operazione di media. Possiamo allora scrivere:

$$\Psi_{F}(R) \propto \lim_{t \rightarrow \infty} \sum_P(-1)^P... ...t \langle \exp{ -\int_0^t E_n [ R(t') ]} \right \rangle_{DRW}$$ (3.10)

Non sappiamo risolvere analiticamente le medie sul random walk, possiamo approssimare un tempo piccolo 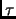$\tau$ la soluzione come:

$$\left \langle \exp{ -\int_0^t E_n [ R(t') ]} \right \rangle_{DRW} \simeq e^{-\tau E^{(n)}[R(0)]}$$ (3.11)

Quindi la nostra funzione d'onda dopo un tempo 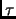$\tau$ diverrà:

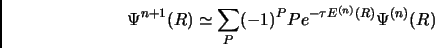$$\Psi^{n+1}(R) \simeq \sum_P (-1)^P P e^{-\tau E^{(n)}(R)} \Psi^{(n)}(R)$$ (3.12)

Vediamo subito che, ad esempio se partiamo da una funzione di tipo Hartree fatta di onde piane, dopo la prima iterazione otteniamo una funzione antisimmetrica di tipo Jastrow-Slater. Facciamo adesso evolvere la nostra funzione Jastrow-Slater: calcolando l'energia locale si ottiene (vedi 3.18):

$$E^{(1)}(R)= \frac{1}{r_s^2}\sum_i \left [k_i^2 + 2ik_i\nabla... ...u(r_{ij})- (\nabla_i\sum_{j \neq i}u(r_{ij}))^2 \right] + V(R)$$

La nuova funzione d'onda al secondo ordine, 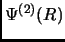$\Psi^{(2)}(R)$ conterrà un'esponenziale complessa, che è il termine di backflow:

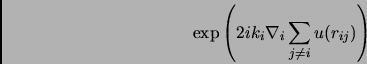$$\exp{ \left(2ik_i\nabla_i\sum_{j\neq i}u(r_{ij})\right)}$$ (3.13)

Esso è in grado di spostare le posizioni dei nodi: infatti se riscriviamo la funzione d'onda come

$$\begin{eqnarray*} \Psi^2(R) &=& \Psi_p(R)det(e^{ik_ir_i})\sum_P(-1)^P e^{\left(2... ...um_{j\neq i}u(r_{ij})\right)} \\ &=& \Psi_p(R)det(e^{ik_ix_i}) \end{eqnarray*}$$

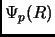dove $\Psi_p(R)$ è un fattore sempre positivo che non cambia mai segno e 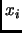$x_i$ è dato da:

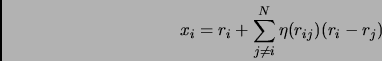$$x_i= r_i + \sum_{j \neq i}^N \eta(r_{ij})(r_i - r_j)$$ (3.14)

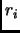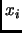il cambiamento delle cordiante nel determinante, dalle $r_i$ alle $x_i$ implica uno spostamento dei nodi della funzione d'onda.
Poiché non sappiamo fare la DRW, scegliamo una funzione variazionale che abbia la corretta dispersione plasmonica simile alla 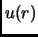$u(r)$. La funzione 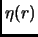$\eta(r)$ è stata scelta nella forma:

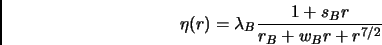$$\eta(r)=\lambda_B \frac{1+s_Br}{r_B +w_Br + r^{7/2}}$$ (3.15)

Dove i parametri 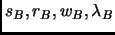$s_B, r_B, w_B, \lambda_B$ sono parametri variazionali e sono stati ottimizzati con una procedura analoga a quella dei parametri del fattore di Jastrow.