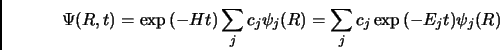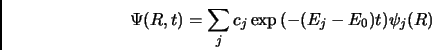Next: Il campionamento d'importanza
Up: Il metodo Monte Carlo
Previous: Variational Monte Carlo
Indice
Indice analitico
Il Diffusion Monte Carlo è un metodo stocastico che proietta una funzione d'onda, non ortogonale allo stato fondamentale, sullo stato fondamentale stesso. Questo metodo si basa sulla soluzione dell'equazione di Schrodinger in tempo immaginario. Consideriamo infatti l'equazione:
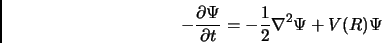 |
(2.3) |
dove
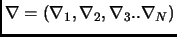 è l'operatore di gradiente N-dimensionale.
Se sviluppiamo la soluzione in autostati dell'Hamiltoniana
è l'operatore di gradiente N-dimensionale.
Se sviluppiamo la soluzione in autostati dell'Hamiltoniana 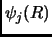 , otteniamo:
, otteniamo:
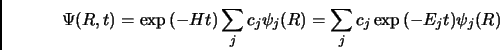 |
(2.4) |
Possiamo ridefinire lo zero dell'energia in modo che:
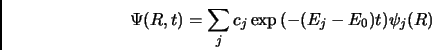 |
(2.5) |
e
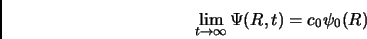 |
(2.6) |
Dove 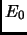 è l'energia dello stato fondamentale. In generale non siamo purtroppo in grado di risolvere l'equazione 2.3;se però trascuriamo il termine di potenziale vediamo che essa si riduce ad un'equazione di diffusione nello spazio delle configurazioni [29]:
è l'energia dello stato fondamentale. In generale non siamo purtroppo in grado di risolvere l'equazione 2.3;se però trascuriamo il termine di potenziale vediamo che essa si riduce ad un'equazione di diffusione nello spazio delle configurazioni [29]:
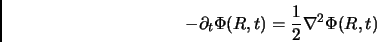 |
(2.7) |
E' possibile calcolare la soluzione dell'equazione di diffusione 2.7, attraverso un insime di cammini casuali nello spazio delle configurazioni walkers che evolvono di moto Browniano secondo l'equazione 2.7, ed acquistano un peso grazie alla presenza di 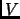 nell'operatore hamiltoniano completo.
Possiamo poi approssimare l'operatore
nell'operatore hamiltoniano completo.
Possiamo poi approssimare l'operatore
![$\exp{[-H\tau]}$](img145.png) per piccoli
per piccoli 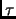 come:
come:
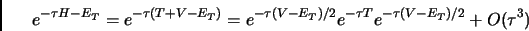 |
(2.8) |
In questo modo il termine cinetico si può trattare come soluzione dell'equazione 2.7 mentre il fattore:
![\begin{displaymath}
P=\exp{[-\tau(V(R)-V(R')-2E_T)/2]}
\end{displaymath}](img147.png) |
(2.9) |
come un peso che viene assegnato a ciascun walker nella sua evoluzione, questo termine si chiama anche branching. Perché storicamente il primo modo di attribuire i pesi veniva realizzato con un algoritmo anch'esso stocastico, che sopprimeva i cammini quando il loro peso era piccolo,e diramava (branch vuol dire ramo) i cammini quando il peso 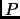 era grande.
era grande.
Subsections





Next: Il campionamento d'importanza
Up: Il metodo Monte Carlo
Previous: Variational Monte Carlo
Indice
Indice analitico
2001-09-28