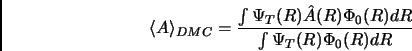Il campionamento d'importanza

La versione del DMC esposta nel precedente paragrafo è molto inefficiente perché il termine di branching 2.9 diverge quando il potenziale, che stiamo utilizzando è singolare, il che con le nostre interazioni coulombiane accade quando gli elettroni si avvicinano troppo fra loro. Ciò produce forti fluttuazioni nei pesi degli walker, e dei valori medi calcolati utilizzando questi ultimi. E' possibile curare questo problema introducendo la funzione 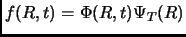$f(R,t)=\Phi(R,t)\Psi_T(R)$, dove 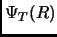$\Psi_T(R)$ è una buona ottimizzazione variazionale e guida il cammino casuale. Infatti l'equazione 2.3 si riscrive come:

$$- \frac{\partial f(R,t)}{\partial t} = - \frac{1}{2} \nabla^2 f(R,t) + \nabla [v_D(R)f(R,t)] + (E_L(R) -E_T)f(R,t)$$ (2.10)

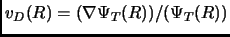dove $v_D(R)=(\nabla \Psi_T(R))/(\Psi_T(R))$ è chiamata velocità di drift e 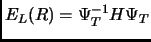$E_L(R)=\Psi_T^{-1}H\Psi_T$ è l'energia locale ottenuta da 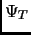$\Psi_T$. Il termine di branching è ora 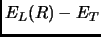$E_L(R)- E_T$, che con una buona scelta di 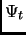$\Psi_t$ varia poco (diverebbe una costante se 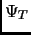$\Psi_T$ coincidesse esattamente con lo stato fondamentale). Il nuovo termine, drift, guida il processo di diffusione verso le regioni in cui 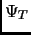$\Psi_T$ è grande, e questo riduce la varianza delle medie se 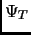$\Psi_T$ è una buona approssimazione dello stato fondamentale.
Quando il processo di diffusione ha raggiunto la distribuzione di equilibrio 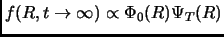$f(R,t \to \infty) \propto \Phi_0(R)\Psi_T(R)$, è possibile valutare il valor medio di un operatore come:

$$\langle A \rangle_{DMC} = \frac{\int \Psi_T(R) \hat A(R) \Phi_0(R)dR}{\int \Psi_T(R) \Phi_0(R)dR}$$

che, nel caso dell'operatore 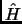$\hat{H}$ coincide proprio con 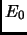$E_0$, energia dello stato fondamentale.