



Next: Optimization Methods
Up: Functional form of the
Previous: Two body Jastrow term
Contents
Three Body Jastrow term
In order to describe well the correlation between electrons the simple two-body
Jastrow factor is not sufficient. Indeed it takes into account only
the electron-electron separation and not the individual electronic position
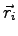 and
and 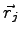 . It is expected that close to atoms the
correlation effects
deviate significantly from the translational invariant Jastrow.
For this reason we introduce a factor, often called three body
(electron-electron-nucleus) Jastrow,
that explicitly depends on both electronic positions
. It is expected that close to atoms the
correlation effects
deviate significantly from the translational invariant Jastrow.
For this reason we introduce a factor, often called three body
(electron-electron-nucleus) Jastrow,
that explicitly depends on both electronic positions
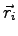 and
and 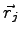 .
The three body Jastrow is chosen to satisfy the
following requirements:
.
The three body Jastrow is chosen to satisfy the
following requirements:
- The cusp conditions set up by the two-body Jastrow term and by the one-body term are preserved.
- Similarly to the two-body we do not include any spin dependency in the three-body Jastrow. In the way the wave-function remains a spin singlet.
- Whenever the atomic distances are large it factorizes
into a product of independent contributions located near each atom,
an important requirement to satisfy the
size consistency of the variational wave function.
Analogously to the pairing trial function in Eq. 1.19
we define a three body factor as:
where indices 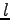 and
and 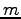 indicate different orbitals located around the atoms
indicate different orbitals located around the atoms 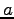 and
and 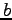 respectively.
Each Jastrow orbital
respectively.
Each Jastrow orbital
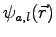 is centred on
the corresponding atomic position
is centred on
the corresponding atomic position 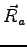 .
We have used Gaussian and exponential orbitals multiplied by appropriate
polynomials of the electronic coordinates, related to different
spherical harmonics with given angular momentum,
as in the usual Slater basis.
.
We have used Gaussian and exponential orbitals multiplied by appropriate
polynomials of the electronic coordinates, related to different
spherical harmonics with given angular momentum,
as in the usual Slater basis.
The chosen form for the 3-body Jastrow (1.28)
has very appealing features: it easily allows to include the
symmetries of the system by imposing them on the matrix
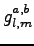 exactly as it is possible for the
pairing part (e.g. by replacing
exactly as it is possible for the
pairing part (e.g. by replacing
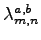 with
with
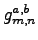 in Eq. 1.20).
It is size consistent, namely the atomic limit
can be smoothly recovered with the same trial function
when the matrix terms
in Eq. 1.20).
It is size consistent, namely the atomic limit
can be smoothly recovered with the same trial function
when the matrix terms
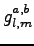 for
for 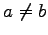 approach zero in this limit (see Ref. (15)). Notice that a small non zero value
of
approach zero in this limit (see Ref. (15)). Notice that a small non zero value
of
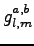 for
for 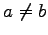 acting on p-wave orbitals
can correctly describe
a weak interaction between electrons such as
the Van der Waals forces.
acting on p-wave orbitals
can correctly describe
a weak interaction between electrons such as
the Van der Waals forces.




Next: Optimization Methods
Up: Functional form of the
Previous: Two body Jastrow term
Contents
Claudio Attaccalite
2005-11-07
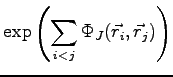
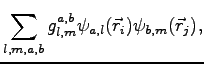
![]() exactly as it is possible for the
pairing part (e.g. by replacing
exactly as it is possible for the
pairing part (e.g. by replacing
![]() with
with
![]() in Eq. 1.20).
It is size consistent, namely the atomic limit
can be smoothly recovered with the same trial function
when the matrix terms
in Eq. 1.20).
It is size consistent, namely the atomic limit
can be smoothly recovered with the same trial function
when the matrix terms
![]() for
for ![]() approach zero in this limit (see Ref. (15)). Notice that a small non zero value
of
approach zero in this limit (see Ref. (15)). Notice that a small non zero value
of
![]() for
for ![]() acting on p-wave orbitals
can correctly describe
a weak interaction between electrons such as
the Van der Waals forces.
acting on p-wave orbitals
can correctly describe
a weak interaction between electrons such as
the Van der Waals forces.