



Next: Gradients and Laplacian
Up: Local Energy and its
Previous: Derivatives of the Local
Contents
In the same spirit of the pairing determinant we built a three-body factor as:
When you move an electron 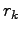 the ratio between the two three-body factor is given by:
the ratio between the two three-body factor is given by:
![$\displaystyle \frac{U(r_k')}{U(r_k)} = \exp \left( \sum_{m,n} { \left [ \sum_{(...
... \right ) + \phi_m(r_k') \phi_n(r_k')-\phi_m(r_k) \phi_n(r_k) \right] } \right)$](img737.png) |
(B.26) |
and if you accept the move to update the value of three-body you have only to update 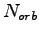 orbitals.
orbitals.
Subsections
Claudio Attaccalite
2005-11-07
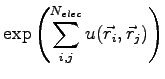
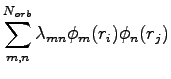
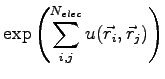
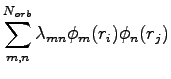
![$\displaystyle \frac{U(r_k')}{U(r_k)} = \exp \left( \sum_{m,n} { \left [ \sum_{(...
... \right ) + \phi_m(r_k') \phi_n(r_k')-\phi_m(r_k) \phi_n(r_k) \right] } \right)$](img737.png)