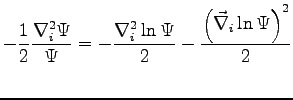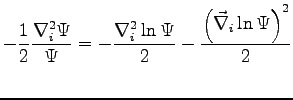Kinetic Energy

To evaluate the kinetic energy we rewrite the the kinetic operator as:

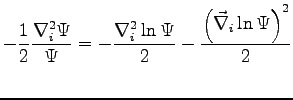$$-\frac{1}{2}\frac{\nabla^2_i \Psi}{\Psi} = - \frac{\nabla^2_i \ln \Psi}{2} - \frac{ \left ( \vec{\nabla}_i \ln \Psi \right )^2 }{2}$$ (B.1)

Because our trial-function is made as product of different terms:

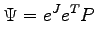$$\Psi = e^J e^T P$$ (B.2)

we can rewrite the kinetic energy through gradients and laplacian of the logarithm of each term, namely:

$$\ln \Psi = J(r_{ij}) + T(r_i,r_j,r_{ij}) +\ln P$$

$$\vec{\nabla}\ln \Psi = \vec{\nabla}J(r_{ij})+ \vec{\nabla}T(r_i,r_j,r_{ij}) + \frac{\vec{\nabla}P}{P}$$

$$\nabla^2 \ln \Psi = \nabla^2 J(r_{ij}) + \nabla^2 T(r_i,r_j,r_{ij}) + \frac{\nabla^2 P}{P} -\left ( \frac{\vec{\nabla}P}{P} \right)^2$$ (B.3)