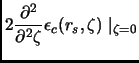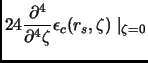Next: Dipendenza dalla densità
Up: Il modello per l'energia
Previous: Il modello per l'energia
Indice
Indice analitico
Per prima cosa abbiamo cercato una rappresentazione semplice per l'energia di scambio e correlazione ad 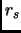 fissato variando la polarizzazione.
fissato variando la polarizzazione.
Sappiamo che:
Vogliamo costruire una funzione che si riduca al limite noto per bassi 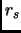 e che invece sia un polinomio biquadratico per
e che invece sia un polinomio biquadratico per 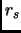 più alti. Cerchiamo quindi una
più alti. Cerchiamo quindi una 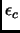 che cancelli a
che cancelli a 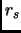 grandi il contributo dei termini di ordine 6 e superiore della
grandi il contributo dei termini di ordine 6 e superiore della 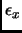 . Tali termini, che indichiamo globalmente con
. Tali termini, che indichiamo globalmente con
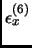 , rappresentano fino allo
, rappresentano fino allo 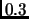 dell'energia di scambio e cioè una quantità molto più grande delle piccole differenze di energia che vogliamo rappresentare per
dell'energia di scambio e cioè una quantità molto più grande delle piccole differenze di energia che vogliamo rappresentare per
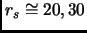 , dove avviene la transizione di fase dal gas paramagnetico al gas polarizzato [31].
Prendiamo una
, dove avviene la transizione di fase dal gas paramagnetico al gas polarizzato [31].
Prendiamo una
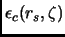 della forma:
della forma:
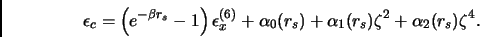 |
(4.2) |
In cui
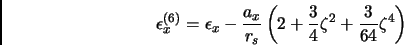 |
(4.3) |
dove
Poiché
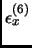 contiene solo potenze di
contiene solo potenze di 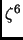 e superiori abbiamo
e superiori abbiamo





Next: Dipendenza dalla densità
Up: Il modello per l'energia
Previous: Il modello per l'energia
Indice
Indice analitico
2001-09-28