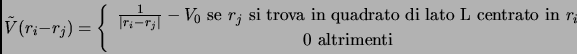Next: Ottimizzazione
Up: L'energia locale
Previous: L'energia cinetica
Indice
Indice analitico
Poiché il nostro sistema ha delle condizioni periodiche al bordo, siamo costretti a sommare il potenziale d'interazione su tutti i vettori del reticolo di Bravais della nostra cella di simulazione; avremo allora:
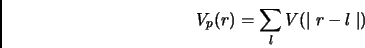 |
(3.18) |
Dove la funzione 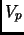 è periodica di periodo
è periodica di periodo 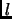 . Per risommare tutta questa serie noi uitlizziamo il Metodo del potenziale troncato. Questo metodo prosto da Fraser [44] ha il vantaggio di non introdurre altri parametri di convergenza (tipo il
. Per risommare tutta questa serie noi uitlizziamo il Metodo del potenziale troncato. Questo metodo prosto da Fraser [44] ha il vantaggio di non introdurre altri parametri di convergenza (tipo il 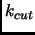 delle somme di Ewald).
Definiamo un potenziale che abbia il corretto limite termodinamico e con media nulla:
delle somme di Ewald).
Definiamo un potenziale che abbia il corretto limite termodinamico e con media nulla:
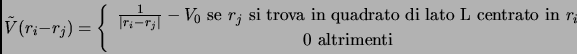 |
(3.19) |
dove 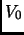 è il valor medio del potenziale sulla nostra cella:
è il valor medio del potenziale sulla nostra cella:
 |
(3.20) |
Questo potenziale in verità non è periodico, ma ha il corretto limite termodinamico ed ad alte densità produce una dipendenza da N minore del potenziale di Ewald (vedi [44,32]).





Next: Ottimizzazione
Up: L'energia locale
Previous: L'energia cinetica
Indice
Indice analitico
2001-09-28