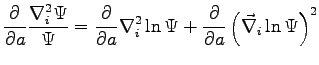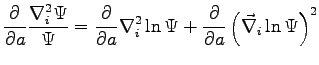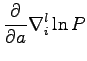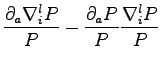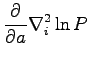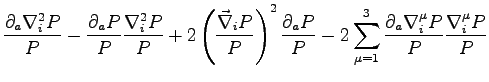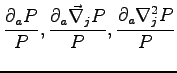Derivatives of the Kinetic Energy

Next: Pairing determinant Up: Kinetic Energy Previous: Kinetic Energy Contents

Derivatives of the Kinetic Energy

We want to calculate the derivatives of the Kinetic Energy respect to a variational parameter of the wave-function:

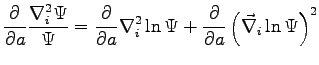$\displaystyle \frac{\partial}{\partial a }\frac{\nabla^2_i \Psi}{\Psi} = \frac{... ... \Psi + \frac{\partial}{\partial a } \left ( \vec{\nabla}_i \ln \Psi \right )^2$

(B.4)

using B.3 we have that:

$\displaystyle \frac{\partial}{\partial a } \nabla^2_i \ln \Psi$	$\displaystyle =$	$\displaystyle \frac{\partial}{\partial a } \left ( \nabla^2_i \ln e^J + \nabla^2_i \ln e^T + \nabla^2_i \ln P \right )$	(B.5)
	$\displaystyle =$	$\displaystyle \frac{\partial}{\partial a } \nabla^2_i J + \frac{\partial}{\partial a } \nabla^2_i T + \frac{\partial}{\partial a } \nabla^2_i \ln P$

and

$\displaystyle \frac{\partial}{\partial a } \left ( \vec{\nabla}_i \ln \Psi \rig... ...right ) \right ] \left ( \nabla_i^l J + \nabla_i^l T + \nabla_i^l\ln P \right )$

(B.6)

For the pairing determinant the terms we have to evaluate will be:

$\displaystyle \frac{\partial}{\partial a } \nabla_i^l \ln P$	$\displaystyle =$	$\displaystyle \frac{\partial_a \nabla_i^l P }{P} - \frac{\partial_a P}{P} \frac{\nabla_i^l P }{P}$
$\displaystyle \frac{\partial}{\partial a } \nabla_i^2 \ln P$	$\displaystyle =$	$\displaystyle \frac{\partial_a \nabla_i^2 P }{P} - \frac{\partial_a P}{P}\frac{... ... -2 \sum_{\mu=1}^3 \frac{\partial_a \nabla_i^\mu P}{P} \frac{\nabla_i^\mu P}{P}$

So to evaluate the gradient of the local energy we need only to know these vectors:

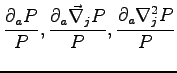$\displaystyle \frac{\partial_a P}{P},\frac{\partial_a \vec{\nabla}_j P}{P},\frac{\partial_a \nabla^2_j P}{P}$

(B.7)

Next: Pairing determinant Up: Kinetic Energy Previous: Kinetic Energy Contents

Claudio Attaccalite 2005-11-07