Dealing with Quantum Monte Carlo noise

Recently different method were proposed to evaluate forces by Quantum Monte Carlo with a finite and small variance (29),(52),(86) (see also section 1.1.1 for a discussion about zero-variance principle).
It is well known that noisy forces can be used in different way for obtaining, following a first order stochastic differential equation, the Canonical distribution. For instance it is possible to use the Langevin dynamic defined by:

$$\dot{x_i} = \beta_{ij}\left ( - \frac{ \partial V}{\partial x_j} + \eta_j \right )$$ (5.1)

$$\langle \eta_i(t) \rangle =$$ 0 (5.2)

$$\langle \eta_i(t) \eta_j(t') \rangle = \alpha_{ij}(x)\delta(t-t'),$$ (5.3)

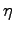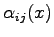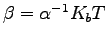where $\eta$ is a random noise with variance $\alpha_{ij}(x)$ and zero mean. It is easy to show, using the Fokker-Plank equation associated to this equation, that in order to obtain the usual Boltzmann distribution the matrix $\beta$ has to be chosen as $\beta = \alpha^{-1} K_b T$ . The problem to obtain the desired canonical distribution may be therefore solved in this way. In QMC one can calculate the covariance matrix 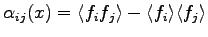$\alpha_{ij}(x) = \langle f_i f_j \rangle - \langle f_i \rangle \langle f_j \rangle$ and then invert this matrix to obtain 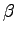$\beta$ and continue the dynamics. This method is unfortunately very unstable, because the matrix 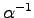$\alpha^{-1}$ can be ill-defined because of statistical fluctuations. Moreover it is not possible to estimate the error on the temperature simulated.
Here we present a new method that uses these QMC forces to perform a Molecular Dynamics at finite temperature. In the past the major problem of using QMC to perform ab-initio Molecular Dynamic was the presence of the statistical noise, but now we will show that this noise can be efficiently used as thermal bath. We called this method Generalized Langevin Dynamics by Quantum Monte Carlo (GLQ).
In our simulation there exists a correlated noise associated to the forces. We rely on the central limit theorem implying the noise in all component of the forces evaluated by QMC is Gaussian with a given covariance matrix. We used the Jackknife re-sampling method (see Appendix A) to estimate the covariance matrix.
The idea of the GLQ is to use this noise to produce a given finite temperature using a Generalized Langevin Equation. The use of the Generalized Langevin Equation (GLE) as thermostat is not new. In the past some authors have used this approach to simulate different systems. This method was applied for the fist time by Schneider and Stoll (87), to study distortive-phase transitions. Later the GLE was used to simulate different systems and also to stabilize the usual Molecular Dynamic method (88).